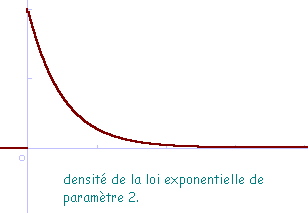
Loi exponentielle

Soit $\lambda$ un réel strictement positif.

La fonction $f$ définie sur $[0;+\infty[$ par $http://latex.codecogs.com/gif.latex?f%28t%29%3D%5Clambda%20e%5E%7B-%5Clambda%20t%7D$ est la densité d'une loi de probabilité, appelée loi exponentielle de paramètre $\lambda$ .

Soit $X$ une variable aléatoire suivant une loi exponentielle de paramètre $\lambda$ .

Pour tout réel $t$ positif :

$P(X\leq t)=\int_0^t-\lambda e^{-\lamnda x}\ \mathrm dx=1-e^{-\lambda t}$

$P(X\geq t)=e^{-\lambda t}$

ROC : pour tous réels $t$ et $h$ positifs (on dit que cette loi porte aussi le loi de durée de vie sans vieillissement ou loi sans mémoire ce qui est justifié par l'égalité suivante. Dans ce cas l'espérance peut s'interpréter comme la durée de vie moyenne) :

$P_{X\geq t}(X\geq t+h)=P(X\geq h)$

ROC : $X$ admet une espérance $E(X)$ définie par :

$E(X)=\lim_{x\to+\infty}\int_0^x(t\lambda e^{-\lambda t})\ \mathrm dt = \frac{1}{\lambda}$

$X$ admet une espérance $V(X)$ définie par :

$V(X)=\lim_{a\to +\infty}\left(\int_0^ax^2f(x)\mathrm dx-(E(x))^2\right)=\frac{1}{\lambda^2}$

Démonstrations.

1. Soit $t\geq 0 \mbox{}$ alors :

$P(X\leq t)=\int_0^t\lambda e^{-\lamnda x}\ \mathrm dx=\[-e^{-\lambda x}\]^t_0=-e^{-\lambda t}+1=1-e^{-\lambda t}$ .

2. $http://latex.codecogs.com/gif.latex?P%28X%5Cgeq%20t%29%3D1-P%28X%3Ct%29$ . Or $X$ est une variable aléatoire continue donc $P(X<t)=P(X\leq t)$ . Ainsi : $P(X\leq t)=1-1+e^{-\lambda t}=e^{-\lambda t}$ .

3. ROC. En s'aidant du 2. :

$\\ P_{X\geq t}(X\geq t+h)=\frac{P((X\geq t+h)\ et\ (X\geq t))}{P(X\geq t)}=\frac{P(X\geq t+h)}{P(X\geq t)}.\ \mbox{Ainsi :}\\ P_{X\geq t}(X\geq t+h)=\frac{P(X\geq t+h)}{P(X\geq t)}=\frac{e^{-\lambda(t+h)}}{e^{-\lambda t}}=e^{-\lambda h}=P(X\geq h)$

4. ROC. Posons $F(t)=-te^{-\lambda t}-(1/\lambda )e^{-\lambda t}$ pour tout $t\in[0;+\infty[$ . $F$ est dérivable sur $[0;+\infty[$ et on a (par calculs successifs) :

$F'(t)=t\lambda e^{-\lambda t}-e^{-\lambda t}-(1/\lambda)(-\lambda)e^{-\lambda t}=t\lambda e^{-\lambda t}$ , ce qui prouve que $F$ est une primitive de $t \mapsto t\lambda e^{-\lambda t}$ .

Limite de $F$ en $+\infty$ :

$\\ \bullet \lim_{t\to +\infty}-t e^{-\lambda t}=\lim_{t\to+\infty}((1/\lambda)-t\lambda e^{-\lambda t})\stackrel{X=-t\lambda}{=}\lim_{X\to -\infty}((1/\lambda) Xe^X)=0\\ \bullet \lim_{t\to+\infty}e^{-\lambda t}=0$

Par addition :

$\lim_{t\to +\infty}F(t)=0$

On a donc :

$E(x)=\lim_{x\to +\infty}(F(x)-F(0))=-F(0)=-\frac{1}{\lambda}$

4. Même principe pour la variance.

On aurait pu aussi intégrer par parties dont la méthode est plus simple, ou chercher une relation entre la fonction et sa/ses dérivée(s) ou enfin la factorisation par un polynôme avec la fonction exponentielle. Au total, il existe, au moins, quatre méthodes qui sont détaillées dans le ROC n°12.