- Accueil
- Les suites
- Les fonctions
- Fonctions trigonométriques
- Fonction exponentielle
- Les nombres complexes
- Probabilités
- Logarithme népérien
- Primitives et intégration
- Lois continues
- Géométrie dans l'espace
- Lois normales (avec échantillonnage)
- R.O.C
- Exercices de bac
- Exercices à prise d'initiatives
- Bac 2015
- Rappels
- Contactez-moi
Notions de limites
Une suite est convergente lorsqu'elle admet une limite finie.
Une suite est divergente lorsqu'elle admet une limite infinie ou lorsqu'elle n'a pas de limite.
Exemple : la suite :
n'admet pas de limite finie, elle
diverge.
La suite converge vers un réel
, si tout intervalle ouvert comportant
contient tous les termes de la suite à partir d'un certain rang. En
d'autres termes :
.
En somme, on trouvera tous les termes de la suite, à partir d'un certain rang, dans un intervalle ,
étant un réel. Voir image ci-dessous :
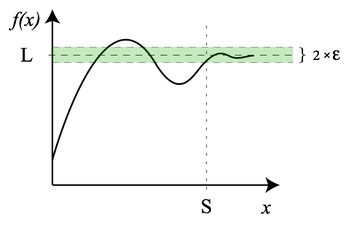
La suite tend vers
, si tout intervalle de la forme
,
étant un réel, contient toutes les valeurs
à partir d'un certain rang. Entre d'autres termes :
.
Exemple : la suite :
.
La suite tend vers
, si tout intervalle de la forme
,
étant un réel, contient toutes les valeurs
à partir d'un certain rang. Entre d'autres termes :
.
Exemple : la suite .
À partir d'un certain rang, si une suite converge vers un réel non nul, alors elle est du signe de
. La démonstration réside sur la définition en elle-même. On sait que, d'après la définition :
.
Si on pose :
Si est négatif, alors :
Donc : .
Si est positif, alors :
Donc : .
(Admis) Si la limite existe, alors elle est unique. La démonstration se fait également avec la définition de la limite.