Soient un nombre complexe non nul et son point image. Si et si , alors :

• est le module de , et on le note .
• est un argument de , et on le note .

Voir image ci-dessous qui illustre le tout.

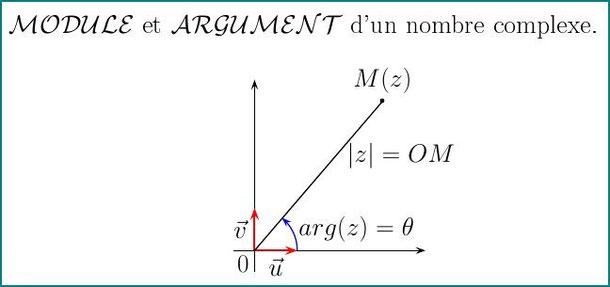
On a les propriétés suivantes :

• est un réel strictement positif si .
• est un réel strictement négatif si .
• est un réel non nul si
• est un imaginaire pur si

Soit un nombre complexe non nul, l'écriture suivante avec  et est appelée forme trigonométrique.

Si on connaît la forme trigonométrique de : , alors : .

Si on connaît la forme algébrique, on a alors, avec :

Propriétés des modules :

1. 
2. 
3. 
4. 
5. avec
6. 

Exemple de démonstration :
On connaît le point 2. On peut écrire : .

Propriétés des arguments :

Exemple de démonstration :

On peut écrire :