Théorème des valeurs intermédiaires

Une fonction $f$ continue sur un intervalle $[a;b]$ (avec $b>a$ ) atteint toutes les valeurs comprises entre $f(a)$ et $f(b)$ c'est-à-dire : pour tout réel $k$ compris entre $f(a)$ et $f(b)$ , il existe au moins un réel $c$ de l'intervalle $[a;b]$ tel que $f(c)=k$ .

Une étude complète de la fonction (sens de variations, extremums, etc.) permet de déterminer le nombre exact de solutions.

Démonstration : elle peut se faire par dichotomie. Pour une démonstration très complète et détaillée, voir ici

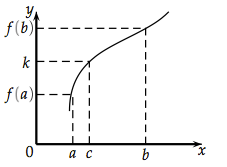
Théorème de la bijection : une fonction $f$ continue et strictement monotone sur un intervalle $[a;b]$ (avec $b>a$ ) atteint toutes les valeurs comprises entre $f(a)$ et $f(b)$ (soit $f([a;b])=[f(a);f(b)]$ , car la fonction est strictement monotone), c'est-à-dire : pour tout réel $k$ compris entre $f(a)$ et $f(b)$ , il existe un unique réel $c$ de l'intervalle $[a;b]$ tel que $f(c)=k$ .

L'image d'un intervalle $I$ par une fonction continue est un intervalle. Soit : $f([a;b])=[f(a);f(b)]$ (dans le cas d'un intervalle fermé mais ça revient au même s'il était ouvert).

Démonstration.

Si $x$ et $y$ sont des éléments de $f(I)$ , alors tout nombre $z$ vérifiant $x<z<y$ est encore dans $f(I)$ (propriété des intervalles).

Puisque $x$ et $y$ sont des éléments de $f(I)$ , on a donc deux nombres $a$ et $b$ dans $I$ tels que : $x=f(a)$ et $y=f(b)$ . Puisque la fonction est continue, le théorème des valeurs intermédiaires prouve qu'il existe un nombre $c$ dans $I$ tel que $f(c)=z$ (puisque $z$ est compris entre $f(a)$ et $f(b)$ ). Donc : $z\in f(I)$ . Ce qu'il fallait démontrer.