- Accueil
- Les suites
- Les fonctions
- Fonctions trigonométriques
- Fonction exponentielle
- Les nombres complexes
- Probabilités
- Logarithme népérien
- Primitives et intégration
- Lois continues
- Géométrie dans l'espace
- Lois normales (avec échantillonnage)
- R.O.C
- Exercices de bac
- Exercices à prise d'initiatives
- Bac 2015
- Rappels
- Contactez-moi
Correction
Exercice 1 :
1. Soit .
a. Il est évident que : et
. Par addition :
b.
c. Il est évident que sur
, donc la fonction
est strictement croissante sur
2. Soit la fonction définie sur :
a. Il est évident que : et
, indépendant de la
valeur de
. On a donc :
b. Étudions le signe de la dérivée. On a :
Il est évident que et
, donc, il en résulte :
(addition de termes positifs) sur
. La
fonction
est strictement croissante sur
.
c. On sait que la fonction est strictement croissante sur
. De
plus, la fonction
est continue (ajout de fonctions continues et la fonction est
dérivable, donc continue). Enfin, puisqu'elle est strictement croissante, on a :
. La valeur de
est indépendant de
. Il est donc évident que :
.
Le théorème de la bijection dit alors qu'il existe une unique solution telle que
. On a, ainsi :
, l'unique
solution.
d. On a montré que : . On a bien :
(puisque
). On a également :
Or, on sait : (entier naturel non nul). Par passage à
l'inverse :
. Il est
évident que :
, donc, il existe une unique valeur
, tel que
. Ainsi, on a bien :
.
3. On sait que vérifie
l'équation :
(équation
)
Et on sait que :
En soustrayant membre à membre :
Soit, en mettant sur le même dénominateur :
Donc :
Ainsi, on a bien : .
4.
a. On a montré que : . Or, on sait que :
, donc :
. Puisque la fonction
est croissante, on a :
. La suite
est bien croissante.
b. On sait que la suite est bornée (cf. 2.d), donc majorée (ici, par 1) et elle est croissante, la suite
converge. On a donc :
c. On a :
d. On en déduit :
Exercice 2 :
Il advient que l'équation de la tangente s'écrit :
Soit, en développant :
Cette tangente coupe l'axe des abscisses, il est évident que : .
Ainsi :
Ce qu'il fallait montrer.
Exercice 3 :
Soit le polynôme . Le polynôme est une somme de fonctions continues, donc la
fonction
est continue. Il est évident que la fonction
est définie sur
, donc on a :
.
On sait que :
Supposons que et le polynôme de degré impair :
Ici, il est évident que , donc, d'après le théorème des valeurs intermédiaires, il existe au moins une solution telle que
. Le polynôme de degré impair admet bien au moins une racine et ce, quelque soit
soit impair.
Supposons que et le polynôme de degré impair :
Là aussi, il est évident que , donc, d'après le théorème des valeurs intermédiaires, il existe au moins une solution telle que
. Le polynôme de degré impair admet bien au moins une racine et ce, quelque soit
soit impair.
Dans tous les cas, un polynôme de degré impair admet au moins une racine quelque soit impair.
Exercice 4 :
Il suffit de trouver un contre-exemple. Par exemple, n'admet pas de racine.
Exercice 5 :
On sait que converge, donc :
De plus, on a la relation de récurrence suivante :
Posons : . Il
est évident que la fonction est continue (polynôme donc continue, plus soustraction de fonctions continues ). Ainsi, on a :
Ainsi, d'après le théorème du point fixe, on a l'équation suivante :
Ainsi :
(Règle de l'équation produit nul). On serait tenté de diviser par , mais
est-il non nul ?
Ainsi : (puisque la suite est croissante et le premier terme est
positif). Donc :
Remarque : une étude approfondie de la suite aurait permis de montrer qu'elle est croissante et majorée, donc qu'elle converge.
Exercice 6 :
Voyons si l'accroissement admet une limite quand tend vers 0.
On a :
Ainsi, on obtient :
On peut distinguer les cas quand est positif ou négatif mais le résultat est le même.
Donc, la fonction est dérivable en 0, et on a :
.
Exercice 7 :
Il faut raisonner par disjonction de cas pour positif et
négatif. On pourra aboutir à une contradiction.
Exercice 8 :
Vrai, la fonction cube est impaire. On a :
.
Faux, on a :
Exercice 9 :
1.
a. (Rédaction sommaire, juste pour les idées) On étudie le signe de la dérivée. On a :
On remarque que est du signe de
. On a :
pour tout :
. Ainsi, on a :
pour tout
. Donc
est croissante sur
.
pour tout
. Donc
est décroissante sur
.
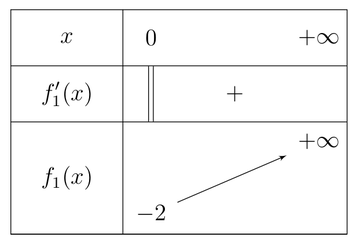
On a donc le tableau de variation suivant :

b. Trivial.
2.
a. On note la proposition pour tout
. On a :
.
Initialisation: montrons que est vraie.
Le proposition est vraie au rang 1.
Hérédité : supposons qu'il existe un entier tel que
soit vraie. Démontrons que
est vraie; c'est-à-dire :
.
On a montré que sur la fonction
est croissante, on a donc :
.
Or :
On a donc : .
La proposition est vraie au rang .
Conclusion : la proposition est vraie au rang 1 et est héréditaire donc elle est vraie pour tout entier naturel non nul.
b. Étudions le signe de . On a :
Or on a vu que pour tout :
. Puisque
pour tout
. Ainsi, on a :
.
Soit :
pour tout
.
c. Puisque , d'après la
question précédente, on a :
. Ainsi :
. La
suite
est décroissante à partir du rang 1 pour tout entier
naturel non nul.
d. La suite est décroissante et est minorée par
, donc, d'après le théorème, la suite
converge vers un réel
.
3. On sait que est continue (somme de fonctions continues) sur
, donc
est continue en
. De plus, la suite converge, on a donc :
.
De plus, on a :
D'après le théorème du point fixe, on a : . Ainsi, cela revient à résoudre l'équation :
Après mise en équation et résolution (triviale), on obtient : ou
. Puisque la suite est strictement positive (cf. 2.a), la seule limite possible est :
.