- Accueil
- Les suites
- Les fonctions
- Fonctions trigonométriques
- Fonction exponentielle
- Les nombres complexes
- Probabilités
- Logarithme népérien
- Primitives et intégration
- Lois continues
- Géométrie dans l'espace
- Lois normales (avec échantillonnage)
- R.O.C
- Exercices de bac
- Exercices à prise d'initiatives
- Bac 2015
- Rappels
- Contactez-moi
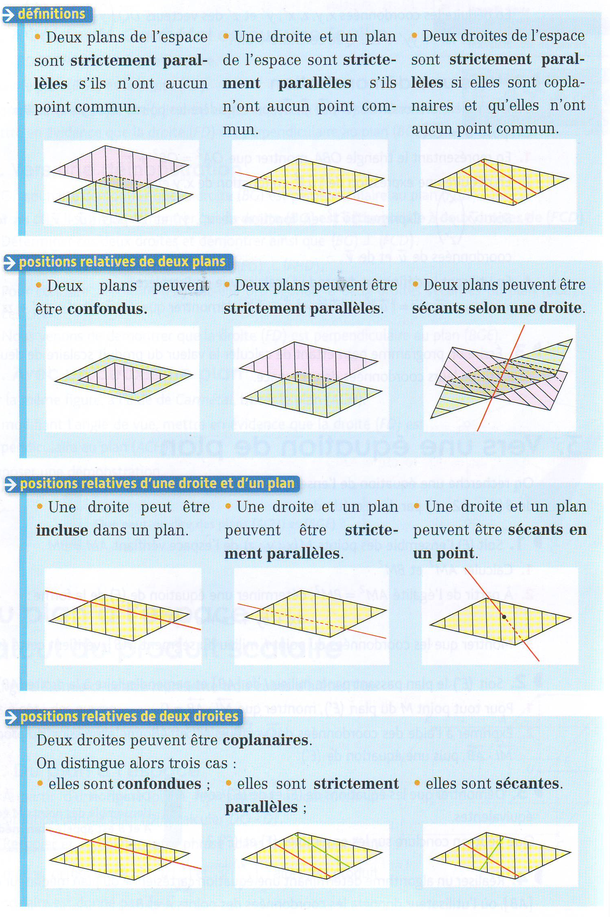
Parallélisme dans l'espace
Définition :
Deux plans de l'espace sont strictement parallèles s'ils n'ont aucun point en commun.
Une droite et un plan de l'espace sont strictement parallèles s'ils n'ont aucun point en commun.
Deux droites de l'espace sont strictement parallèles si elles sont coplanaires et si elles n'ont aucun point en commun.
Positions relatives de droites et plans de l'espace (par mathsrepère, édition Hachette 2012) :
Montrer que deux plans sont parallèles :
- 2 plans parallèles à un même plan 3e plan sont parallèles entre eux.
- Si deux droits sécantes d'un plan
sont respectivement parallèles à deux droites sécantes d'un plan
alors
.
Montrer qu'une droite et un plan sont parallèles :
- si une droite
est parallèle à une droite contenue dans un plan
, alors
.
- Si deux plans
et
sont parallèles et si la droite
est contenue dans le plan
, alors
est parallèle au plan
.
Montrer que deux droites sont parallèles :
- Si deux plans sont parallèles alors tout plan qui coupe l'un coupe aussi l'autre et les intersections sont deux droites parallèles.
-
Théorème du toit : si
et
sont deux plans sécants selon une droite
et si une droite
contenue dans
est parallèle à une droite
contenue dans
, alors
est parallèle à
et
.