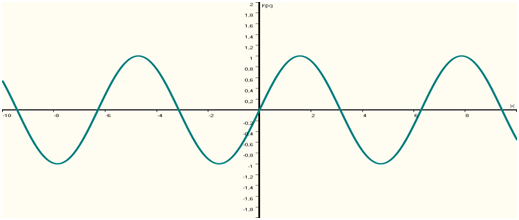
Fonctions sinus et cosinus

Pour tout réel $x$ , on a :

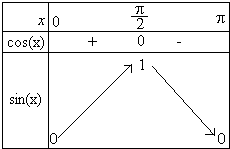
Démontrables grâce au cercle trigonométrique et aux définitions (source : jybaudot.com) :

Périodicité : les fonctions cosinus et sinus sont $2\pi$ -périodiques, c'est-à-dire :

$\forall k\in \mathbb{Z}, \cos(x)=\cos(x+2k\pi)\ et\ \sin(x)=\sin(x+2k\pi)$

Parité : on a : $\cos (x)=\cos (-x)$ et $\sin (x)=-\sin (x )$ . La fonction cosinus est paire, la fonction sinus est impaire.

On a :

$\lim_{x\to 0}\frac{\sin x}{x}=1$ et $\lim_{x\to 0}\frac{\cos x-1}{x}=0$

Ces formules sont démontrables (en passant par le nombre dérivé) mais elles ne sont uniquement à apprendre.

Théorème : les fonctions cosinus et sinus sont dérivables sur $\mathbb{R}$ et pour tout réel $http://latex.codecogs.com/gif.latex?x$ :

$\cos'x=-\sin x\ et\ \sin'x=\cos x$

On démontre facilement ces résultats en s'aidant des formules ci-dessus.

Plus généralement, on a :

$\cos'u=-u'\sin u\ et\ \sin'u=u'\cos u$

Démontrable avec le théorème des fonctions composées.

Représentation graphique des fonctions sinus et cosinus (source : jybaudot) :