- Accueil
- Les suites
- Les fonctions
- Fonctions trigonométriques
- Fonction exponentielle
- Les nombres complexes
- Probabilités
- Logarithme népérien
- Primitives et intégration
- Lois continues
- Géométrie dans l'espace
- Lois normales (avec échantillonnage)
- R.O.C
- Exercices de bac
- Exercices à prise d'initiatives
- Bac 2015
- Rappels
- Contactez-moi
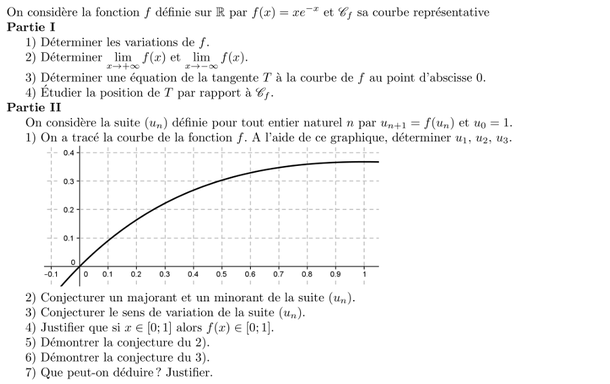
Quelques exercices
NB : les étoiles constituent le niveau de difficulté.
est un exercice facile.
est un exercice moyen.
est un exercice difficile (généralement appelé
"problème ouvert")
Exercice 1 :
Soit la fonction définie sur
par :
.
Étudier-la convenablement.
Exercice 2 :
Soit la fonction définie sur
par :
Étudiez convenablement la fonction : limites, variations, le nombre de racines, le signe.
Exercice 3 (problème bac) :
Soit la fonction définie sur
par :
et
.
Partie A :
1. Démontrer que la droite
d'équation
est asymptote à la
courbe représentative de la fonction.
2. Pour , calculer :
Étudier la limite de cette expression quand tend vers 0. Aide : on pourra utiliser, pour un entier
naturel
non nul :
Que peut-on en déduire ?
3. Démontrer que pour tout , on a :
4. Étudier les variations de la fonction et dresser son tableau de variations.
Partie B :
On note la fonction définie sur
par :
1. Montrer que dans , les
équations
et
sont équivalentes.
2. Démontrer que admet une seule racine réelle
dont on donnera un encadrement à
près.
3. On pose :
Encadrer (en justifiant). Montrer que :
.
4. Pour tout , on note
la tangente à la courbe représentative de la
fonction au point d'abscisse
. Montrer que
a pour équation
.
5. Déduire des questions précédentes que de toutes les tangentes à la courbe représentative de la fonction, seule
passe par l'origine O.
Exercice 4 (extrait d'un problème bac) :
Soit la fonction définie sur
par
:
1. Étudier les variations de et déterminer ses limites aux bornes de
. Existe-t-il une droite asymptote ? Si oui, donner ses
caractéristiques.
2. Écrire l'équation de la tangente en un point d'abscisse
.
3. Montrer qu'il existe exactement deux tangentes, soit deux valeurs de , telles que ces dernières passent par l'origine O.
Exercice 5 :
Pour des éléments de correction, cliquez ici